FM
FM(Factorization Machine)旨在解决稀疏数据下的特征组合问题。CTR模型构建时,对于类别型特征通过先经过one-hot编码成数值型特征,one-hot编码会导致样本特征稀疏,而且特征维度剧增。另外实际使用中,特征交叉之后和点击、购买的相关性更强。如果在one-hot的基础之上做特征交叉,势必造成维度灾难,而且样本的稀疏性会导致交叉特征的权重难以训练。
多项式模型是包含特征组合的最直观模型。在多项式模型当中,特征\(x_{i}\)和\(x_{j}\)的组合采用\(x_{i}x_{j}\)表示,即\(x_{i}\)和\(x_{j}\)均为非零时,组合特征\(x_{i}x_{j}\)才有意义。模型的表达式如下:
\begin{equation} y(X) = \omega_{0} + \sum_{i=1}^{n} \omega_{i}x_{i} + \sum_{i=1}^{n}\sum_{j=i+1}^n \omega_{ij}x_{i}x_{j} \label{eq:poly}\tag{1} \end{equation}
其中,\(n\)代表样本的特征数量,\(x_{i}\)是第\(i\)个特征的值,\(\omega_{0}、\omega_{i}、\omega_{ij}\)是模型参数。
从公式\eqref{eq:poly}可以看出,组合特征的参数一共有\(\frac{n(n-1)}{2}\)个,任意两个参数都是独立的。要训练参数\(\omega_{ij}\)需要大量\(x_{i}\)和\(x_{j}\)都非零的样本,由于样本数据本来就很稀疏,满足”\(x_{i}\)和\(x_{j}\)都非零”的样本就更少了。训练样本不足势必会造成参数\(\omega_{ij}\)不准确,影响模型的性能。 那么,如何解决二次项参数的训练问题呢?矩阵分解提供了一种解决思路。在model-based的协同过滤中,一个rating矩阵可以分解为user矩阵和item矩阵,每个user和item都可以采用一个隐向量表示[1]。 比如在下图中的例子中,我们把每个user表示成一个二维向量,同时把每个item表示成一个二维向量,两个向量的点积就是矩阵中user对item的打分。
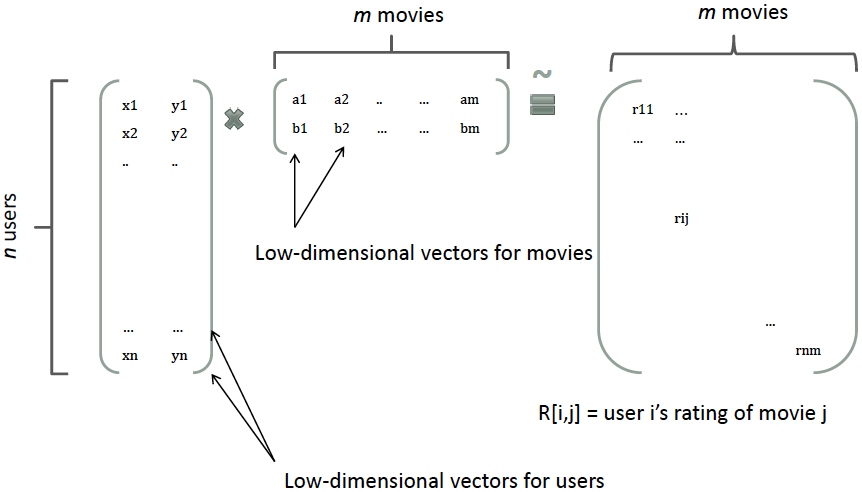
类似地,所有二次项参数 \( w_{ij} \) 可以组成一个对称阵 \( \mathbf{W} \)(为了方便说明FM的由来,对角元素可以设置为正实数),那么这个矩阵就可以分解为 \( \mathbf{W} = \mathbf{V}^T \mathbf{V} \),\( \mathbf{V} \) 的第 \( j \) 列便是第 \( j \) 维特征的隐向量。 换句话说,每个参数 \( w_{ij} = \langle \mathbf{v}_i, \mathbf{v}_j \rangle \),这就是FM模型的核心思想。因此,FM的模型方程为(本文不讨论FM的高阶形式) \[ y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j \label{eq:fm}\tag{2} \]
其中,\( \mathbf{v}_i \) 是第 \( i \) 维特征的隐向量,\( \langle\cdot, \cdot\rangle \) 代表向量点积。隐向量的长度为 \( k \)(\( k << n \)),包含 \( k \) 个描述特征的因子。根据公式\eqref{eq:fm},二次项的参数数量减少为 \( kn \)个,远少于多项式模型的参数数量。另外,参数因子化使得 \( x_h x_i \) 的参数和 \( x_i x_j \) 的参数不再是相互独立的,因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说,\( x_h x_i \) 和 \( x_i x_j \) 的系数分别为 \( \langle \mathbf{v}_h, \mathbf{v}_i \rangle \) 和 \( \langle \mathbf{v}_i, \mathbf{v}_j \rangle \),它们之间有共同项 \( \mathbf{v}_i \)。也就是说,所有包含“\( x_i \) 的非零组合特征”(存在某个 \( j\neq i \),使得 \( x_i x_j \neq 0 \))的样本都可以用来学习隐向量 \( \mathbf{v}_i \),这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中,\( w_{hi} \) 和 \( w_{ij} \) 是相互独立的。
显而易见,公式\eqref{eq:fm}是一个通用的拟合方程,可以采用不同的损失函数用于解决回归、二元分类等问题,比如可以采用MSE(Mean Square Error)损失函数来求解回归问题,也可以采用Hinge/Cross-Entropy损失来求解分类问题。当然,在进行二元分类时,FM的输出需要经过sigmoid变换,这与Logistic回归是一样的。直观上看,FM的复杂度是\(O(kn^2)\)。但是,通过公式\eqref{eq:fm_conv}的等式,FM的二次项可以化简,其复杂度可以优化到\(O(kn)\)[7]。由此可见,FM可以在线性时间对新样本作出预测。
\[ \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum_{f=1}^k \left(\left( \sum_{i=1}^n v_{i, f} x_i \right)^2 - \sum_{i=1}^n v_{i, f}^2 x_i^2 \right) \label{eq:fm_conv}\tag{3} \]
我们再来看一下FM的训练复杂度,利用SGD(Stochastic Gradient Descent)训练模型。模型各个参数的梯度如下
\[ \frac{\partial}{\partial\theta} y (\mathbf{x}) = \left\{\begin{array}{ll}
1, & \text{if}\; \theta\; \text{is}\; w_0 \
x_i, & \text{if}\; \theta\; \text{is}\; w_i \
x_i \sum_{j=1}^n v_{j, f} x_j - v_{i, f} x_i^2, & \text{if}\; \theta\; \text{is}\; v_{i, f}
\end{array}\right. \]
其中,\( v_{j, f} \) 是隐向量 \( \mathbf{v}_j \) 的第 \( f \) 个元素。由于 \( \sum_{j=1}^n v_{j, f} x_j \) 只与 \( f \) 有关,而与 \( i \) 无关,在每次迭代过程中,只需计算一次所有 \( f \) 的 \( \sum_{j=1}^n v_{j, f} x_j \),就能够方便地得到所有 \( v_{i, f} \) 的梯度。显然,计算所有 \( f \) 的 \( \sum_{j=1}^n v_{j, f} x_j \) 的复杂度是 \( O(kn) \);已知 \( \sum_{j=1}^n v_{j, f} x_j \) 时,计算每个参数梯度的复杂度是 \( O(1) \);得到梯度后,更新每个参数的复杂度是 \( O(1) \);模型参数一共有 \( nk + n + 1 \) 个。因此,FM参数训练的复杂度也是 \( O(kn) \)。综上可知,FM可以在线性时间训练和预测,是一种非常高效的模型。
FM与其他模型的对比
FM是一种比较灵活的模型,通过合适的特征变换方式,FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等[3]。 相比SVM的二阶多项式核而言,FM在样本稀疏的情况下是有优势的;而且,FM的训练/预测复杂度是线性的,而二项多项式核SVM需要计算核矩阵,核矩阵复杂度就是N平方。相比MF而言,我们把MF中每一项的rating分改写为\(r_{ui} \sim \beta_u + \gamma_i + x_u^T y_i\),从公式\eqref{eq:fm}中可以看出,这相当于只有两类特征\(u\)和\(i\)的FM模型。对于FM而言,我们可以加任意多的特征,比如user的历史购买平均值,item的历史购买平均值等,但是MF只能局限在两类特征。SVD++与MF类似,在特征的扩展性上都不如FM,在此不再赘述。
FFM
FFM(Field-aware Factorization Machine)最初的概念来自Yu-Chin Juan(阮毓钦,毕业于中国台湾大学,现在美国Criteo工作)与其比赛队员,是他们借鉴了来自Michael Jahrer的论文[4]中的field概念提出了FM的升级版模型。 通过引入field的概念,FFM把相同性质的特征归于同一个field。以上面的广告分类为例,“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征都是代表日期的,可以放到同一个field中。同理,商品的末级品类编码生成了550个特征,这550个特征都是说明商品所属的品类,因此它们也可以放到同一个field中。简单来说,同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field,包括用户性别、职业、品类偏好等。在FFM中,每一维特征\(x_i\),针对其它特征的每一种field \(f_j\),都会学习一个隐向量\(\mathbf{v}_{i, f_j}\)。 因此,隐向量不仅与特征相关,也与field相关。也就是说,“Day=26/11/15”这个特征与“Country”特征和“Ad_type”特征进行关联的时候使用不同的隐向量,这与“Country”和“Ad_type”的内在差异相符,也是FFM中“field-aware”的由来。
假设样本的 \( n \) 个特征属于 \( f \) 个field,那么FFM的二次项有 \( nf \)个隐向量。而在FM模型中,每一维特征的隐向量只有一个。FM可以看作FFM的特例,是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性,可以导出其模型方程。 \[ y(\mathbf{x}) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_{i, f_j}, \mathbf{v}_{j, f_i} \rangle x_i x_j \label{eq:ffm}\tag{4} \] 其中,\( f_j \) 是第 \( j \) 个特征所属的field。如果隐向量的长度为 \( k \),那么FFM的二次参数有 \( nfk \) 个,远多于FM模型的 \( nk \) 个。此外,由于隐向量与field相关,FFM二次项并不能够化简,其预测复杂度是 \( O(kn^2) \)。
下面以一个例子简单说明FFM的特征组合方式[9]。输入记录如下
| User | Movie | Genre | Price |
|---|---|---|---|
| YuChin | 3Idiots | Comedy, Drama | $9.99 |
这条记录可以编码成5个特征,其中“Genre=Comedy”和“Genre=Drama”属于同一个field,“Price”是数值型,不用One-Hot编码转换。为了方便说明FFM的样本格式,我们将所有的特征和对应的field映射成整数编号。
| Field name | Field index | Feature name | Feature index |
|---|---|---|---|
| User | 1 | User=YuChin | 1 |
| Movie | 2 | Movie=3Idiots | 2 |
| Genre | 3 | Genre=Comedy | 3 |
| Price | 4 | Genre=Drama | 4 |
| Price | 5 |
那么,FFM的组合特征有10项,如下图所示。
DNN
在构建ctr模型的时候,会遇到大量的离散特征,譬如商品ID,用户ID。哪怕是稍微简单点儿的商品的类目、用户画像信息,为了充分提取特征而进行的特征交叉也会非常繁琐。因此还是得从模型上入手来自动地进行特征交叉。诚然,树模型(GBDT/XGBOOST)、FM类的模型具有一定的特征交叉能力,但是交叉能力也比较有限,还是要进行各种特征工程,这时候就需要借助DNN类的模型啦。
DNN类的模型的网络结构看上去就具有特征交叉的能力,更重要的是深度神经网络
